type
status
date
slug
summary
tags
category
icon
password
Sub-item
Last edited time
Oct 28, 2023 10:44 AM
Parent item
领域
Schnorr签名的核心是签名算法,对于数学困难的问题,可以基于离散对数,也可以基于椭圆曲线。
基于椭圆曲线
Schnorr签名可以与ECDSA使用同一个椭圆曲线:secp256k1 curve,升级起来的改动非常小。
定义几个变量:
- :椭圆曲线的基点。
- :待签名的数据,通常是一个32字节的哈希值。
- :私钥。,为对应的公钥。
- :哈希函数。写法可理解为:将三个字段拼接在一起然后再做哈希运算。
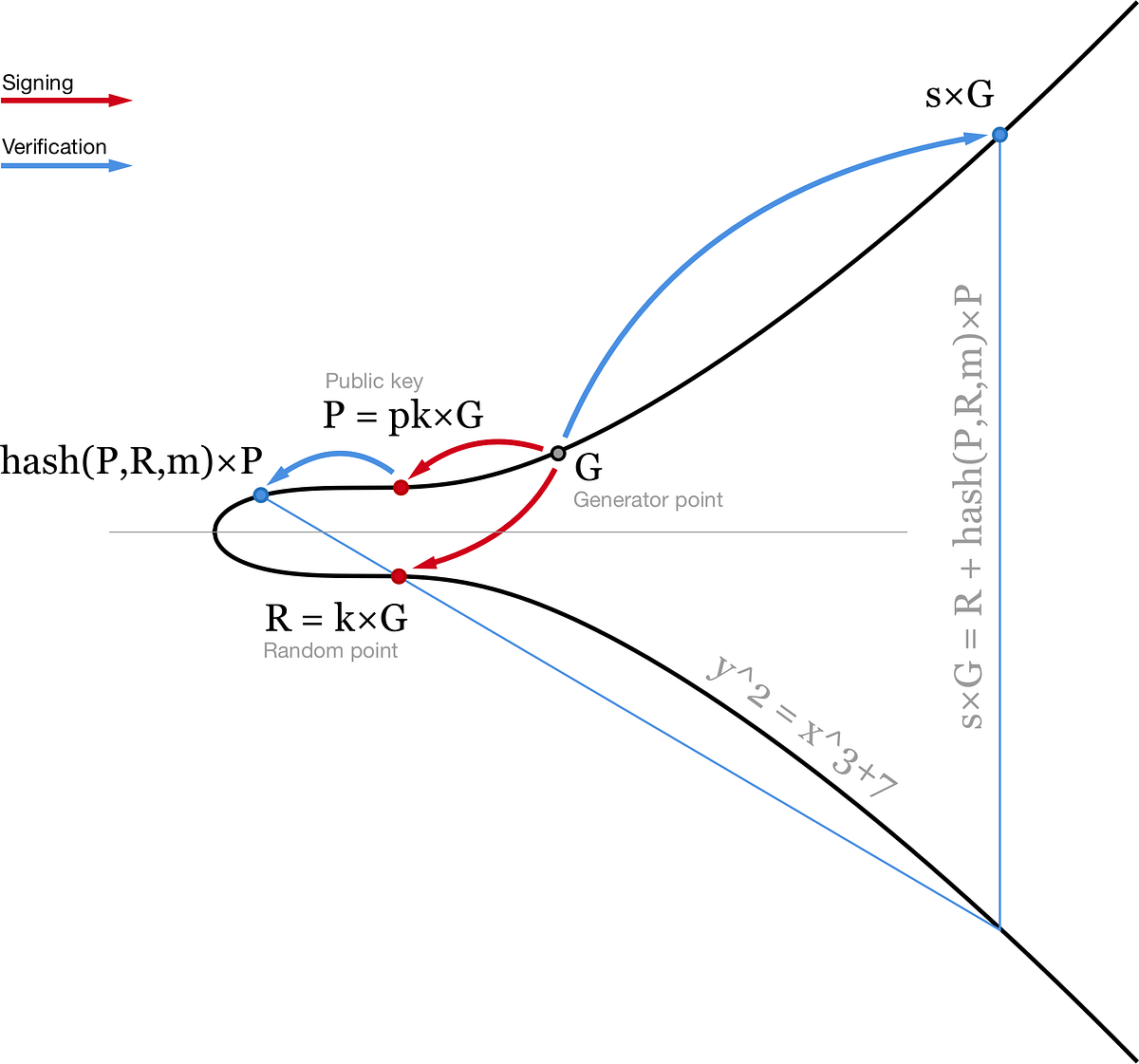
生成签名
- 选择一个随机数,作为临时私钥,令
- 令 , 算式的作用是利用消息的哈希和随机数据对私钥作线性变换,这一点非常重要,是Schnorr多重签名的基础。
那么,公钥对消息的签名就是:,这一对值即为Schnorr签名
生成签名的过程只有加法和乘法,所消耗计算量相比ElGamal会小很多。
验证签名
验证如下等式是否成立:
若等式成立,则可证明签名合法。
我们推演一下,此过程包含了一个极其重要的理论:椭圆曲线无法进行除法运算。
- 值的定义:,等式两边都乘以椭圆曲线,则有:
- ,又因,则有:
椭圆曲线无法进行除法运算,所以第3步的等式,无法向前反推出第1步,就不会暴露值以及私钥。同时,也完成了等式验证。
基于离散对数
签名

验签