type
status
date
slug
summary
tags
category
icon
password
Sub-item
Last edited time
Oct 28, 2023 10:44 AM
Parent item
领域
Schnorr 签名算法的不足:
- 多重签名需要多次(签名者之间的)通信,这对冷钱包来说过于麻烦;
- 聚合签名算法依赖随机数生成器,而不像 ECDSA 那样可以使用指定的随机点(R);
- m-n 多重签名机制比较取巧,需要构建公钥的默克尔树。当 m 和 n 较大时,树所占空间会相当大;
- 无法把一个区块中的所有签名聚合成一个签名。
BLS签名不需要随机数生成器,可以将区块中的所有签名聚合成一个,容易实现 m-n 多重签名,也可以避免签名者之间的多余通信。除此之外,BLS 签名的长度更短(签名为椭圆曲线上的一个点而非两个),是 Schnorr 或 ECDSA 的 2 分之一。
基本概念
- 曲线哈希(hashingto the curve,或译作 “哈希成曲线上的点”)
- ECDSA 和 Schnorr 签名算法中,我们对消息进行哈希计算后,结果(哈希值)是数字,BLS 签名算法则不同,它略微修改了哈希算法,结果对应到椭圆曲线上(的一个点):哈希函数保持不变,将得到的哈希值作为点的 x 值寻找椭圆曲线上的对应点。椭圆曲线有 2²⁵⁶ 个点,而 SHA-256 哈希算法的值也恰好是 256 位。
- 一个有效的 坐标,会对应一正一负两个 坐标(因为和都是曲线上的点),所以有占用2个点, 但有的就不会有点,概率是50%。
- 对消息求哈希时,为确保能在曲线上找到对应的点,可以在消息体后附加一个数,若(寻找对应点)失败则累加该数并重新计算。即如果没有找到对应点,则持续尝试 , 等,直到找到为止。当找到对应点后,在 2 个点中选择 坐标较小的那个作为结果即可。
- 曲线配对(curves pairing)
需要一个特殊的函数,能够把一条(或 2 条不同的)曲线上的两个点 P 和 Q映射为一个数: 。此函数还要有一个重要的特性。即对于未知数 和两个点 、 ,无论哪个点乘以,结果相同(并且不会暴露 的任何相关信息),即:。如此,除了乘数交换仍能保持等式成立外,更进一步,以下所有的交换都要保持等式成立:
配对函数中不能使用任何椭圆曲线(特别是比特币的 secp256k1 椭圆曲线)。我们必须使用非常特殊的曲线(通常出自易于配对的曲线簇),才能保证函数的效率和安全。
BLS签名方案
用代表私钥, 代表公钥,代表要签名的消息。生成 BLS 签名,将消息的哈希结果乘以私钥即可。
签名
- 先对消息求曲线哈希
- 再将获取的结果(曲线坐标点)乘以私钥即可:
大功告成!不需要随机数,不需要额外的步骤,仅仅将哈希结果乘以私钥即可。
签名结果是一个曲线上的点,用压缩的序列化格式保存,只占
33 个字节。验签
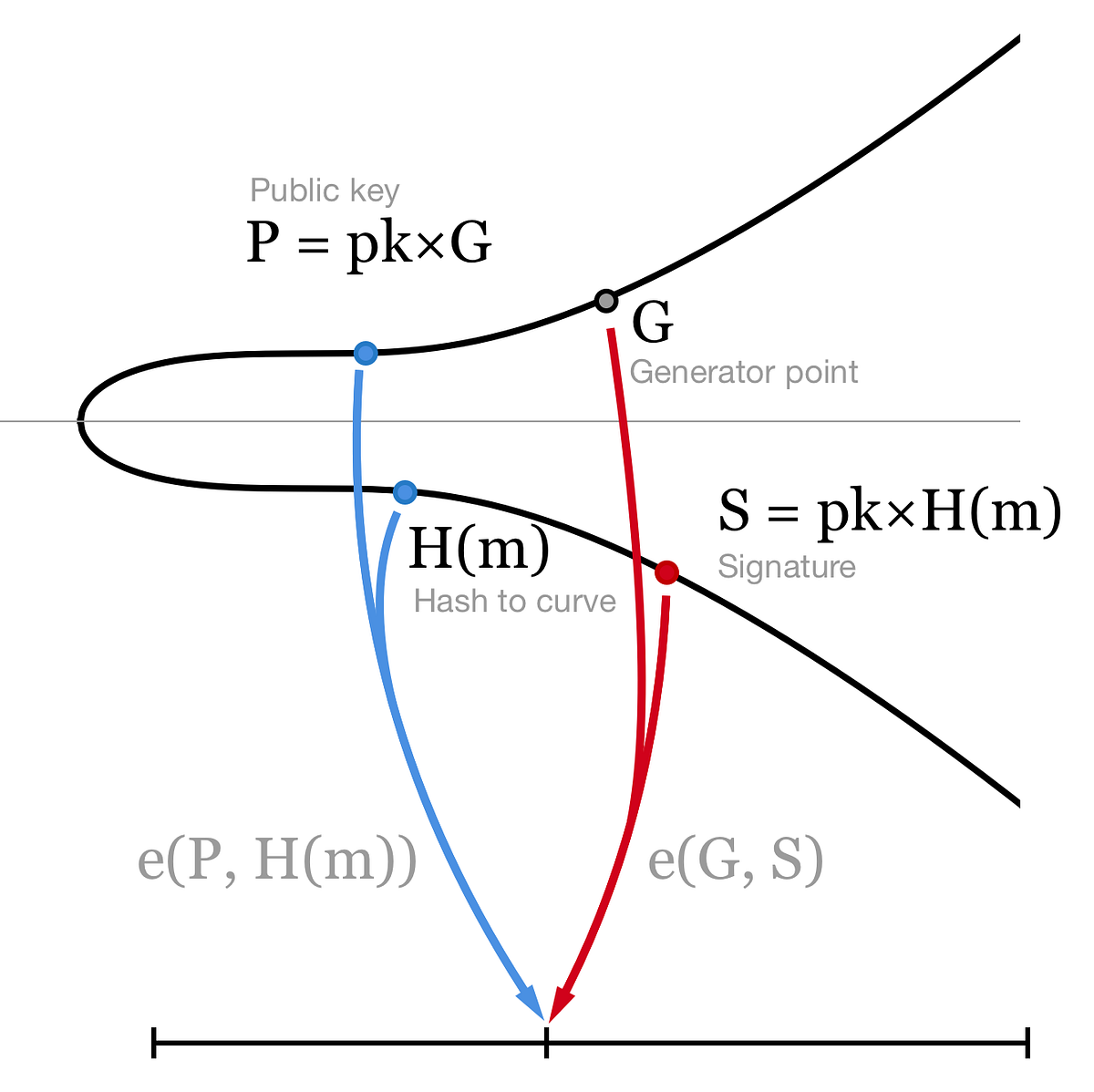
使用公钥 来验证签名,即 。这是为什么呢?
如前所述,配对函数的特性使得如下等式成立:

BLS 签名验证,我们只需验证 公钥和消息的哈希值(曲线上两个点)与曲线生成点和签名(曲线上另两个点)是否映射到同一个数(若是则说明这是一个有效的 BLS 签名)
签名聚合
现在让我们把区块中的签名都聚合在一起。
假设一个区块中有 1000 笔交易,每笔交易都由(签名),(公钥)和 (消息)组成(在这里表示序号)。如果这些签名可以被合并,那又何必分开保存呢?毕竟,我们只关心区块中所有的签名(而不是每一个)是否正确。
聚合签名
为获得聚合签名,只需要将区块中的所有签名加起来:
验证聚合签名
为验证该区块是否正确,我们需要保证以下等式成立:
如果签名都有效,那么该等式的确是成立的,,推导过程如下:
)
这里我们仍需用到所有的公钥,并计算 1001 次配对函数,好处是,区块中的签名只占 33 字节了。签名聚合可以由矿工在挖矿时完成,节省大量的区块空间。
密钥聚合和 n-of-n 多重签名
使用多重签名的地址时,我们会对同一笔交易用不同的密钥进行签名。这种情况下,可以和 Schnorr 算法一样使用聚合密钥,把所有密钥和签名聚合成单个公钥和签名。下面我们以 3-3 多重签名方案为例(同理可推导任意数量的多重签名方案)。
一种简单的聚合方法,是把所有的签名和密钥加起来即可。如此,签名聚合结果为,密钥聚合结果。可以验证以下等式依然成立:
因为:
和 Schnorr 一样,我们也需要杜绝伪造密钥攻击。即在上一篇BLS多重签名中提到的流氓密钥攻击问题。
- 一种方法是要求每个签名参与者证明它拥有公钥对应的私钥(用私钥给公钥签名)。
- 另一种方法是加入非线性系数,使得攻击无法实施。要做到这一点,聚合不再是简单的将多个密钥和签名相加,而是将它们分别乘以某个系数后再相加:
公式中签名和密钥的系数,可以通过签名者以及其它所有人的公钥计算得出,公式如下:
举个例子,可以简单的将签名者的公钥和所有人公钥拼接在一起算出系数:
此时,上面的验证公式依然成立。虽然多了系数,但计算逻辑未变。
该方案的好处是,无需在设备间进行多轮通信,只需知晓其它签名者的相应信息即可。它可比 Schnorr 算法(需要 3 轮通信)的多重签名方案简单多了。这个方案也不依赖随机性,是一种具有完全确定性的签名算法。
子群多重签名方案(m-of-n 多重签名)
多重签名并不常见,我们更倾向使用多重签名(比如多重签名)。我们不想因为丢失( 个密钥中的)一个密钥而一无所有。密钥聚合非常适合这种场景。在 Schnorr 签名算法中,我们用公钥组成的默克尔树来实现密钥聚合,这种方式效率不高,但是将将堪用。不幸地是,当 和 的值变大时,默克尔树的大小会呈指数增长。
BLS 使用了另一种方法,不过略复杂。我们需要一个普通哈希函数(结果为一个数)和一个曲线哈希函数。开始多重签名时,还需要一个初始化过程,这之后,签名者之间就不再需要通信了,只需提供交易签名即可。
举个简单的例子,我们要创建一个 多重签名,3 个签名存储在不同的设备上(这个例子可以扩展为任意的多重签名)。
初始化(生成成员密钥)
用来表示集合中相应位置的设备,用表示私钥,用表示公钥。我们用前面说的方法来聚合公钥:
其中:
现在,每个设备都需要对每个 签名,以证明该是聚合公钥中的一员。将签名聚合后,保存在对应的设备中:
这个签名被称作“成员密钥”,稍后签名时我们会用到。
每个成员密钥都是对消息体的多重签名,即:
因为:
记住这个等式,稍后还会用到。它用来证明某个设备是多重签名中的合法参与者。
签名
假设只用私钥 和 给交易签名,我们会生成 2 个签名 和 :
将它们加起来,聚合成单一的签名和公钥:
用 和,是为了强调它们只是由部分签名者参与计算的(公钥和签名),而不像 那样是由所有签名者参与计算的(公钥)。
验签
为了验证 多重签名,需证明如下等式成立:
上面说过,成员密钥 和 是对消息 和 (消息本身由聚合公钥签名)的签名,所以有:
证明完毕。比多重签名复杂一些,但仍然可以理解。
在比特币中的实现
要在比特币上部署一个 BLS 多签名钱包时,我们需要往某个地址(该地址由聚合公钥 P 生成)打钱。假设我们希望这是一个 2-of-n 多签名合约,那么可以用比特币的锁定脚本来描述,声明如下:
OP_2_ <OP>_OP_CHECK_BLS_MULTISIGOP_2表示需要 2 个密钥进行签名。 这里没有指明总共有 3 个签名,因此它可以表示 2-of-3 或者 2-of-100 等不同的多重签名地址。如此,总签名数永远不会暴露。为了花掉输出(output)地址中的钱,则需要提供
P’(公钥),S’(签名 )以及参与签名者的编号(这个例子中是 1 和 3)。解锁脚本如下:OP_1 OP_3<P'><S'>脚本中有了这些信息,就足够用来验证交易了。其中,
OP_1和 OP_3 告诉我们需要计算的曲线哈希为 H(P, 1)和H(P, 3)。如此,对于任意 m 和 n的多重签名,我们只需要以下信息:
- 一个用在加锁脚本中的聚合公钥 P;
- 一个由部分参与者(m个)生成的聚合公钥 P’(用在解锁中);
- 一个聚合签名 S’;
- 解锁要求的参与者数量m。
一切简单而优美!
由于比特币地址通常只用一次,需要使用 BIP32 这种密钥推导算法生成新的私钥和地址。因此,每次生成新的私钥时,我们也需要生成对应的成员私钥,我不太喜欢这一点。为避免每次交易后都要初始化生成成员私钥,可以一次性地生成一批(比如 1000 个)成员私钥,毕竟每个私钥只占 32 字节。如此,当 1000 个地址用完后,我们才需要再次进行初始化。
不足
配对函数并不那么高效。
BLS 签名验证的复杂度要比 ECDSA 高上一个数量级。 在验证区块中 1000 笔交易的聚合签名时,仍需要进行 1000 次配对计算,这可能比使用 ECDSA 时(对 1000 个单独签名进行验证)还要慢。唯一的好处在于,可以在区块中放更多笔的交易,毕竟聚合签名只占 32 字节。
与 BLS 不同,Schnorr 验证算法的效率很高,它可以把签名放一起验证,效率是 ECDSA 算法的三倍。
配对函数十分复杂,使用不当就会反受其累。一方面,我们希望用高效的配对函数来加快签名验证,另一方面,我们又希望密钥信息暴露越少越好。两者互相矛盾,我们需要异常小心地选择适宜配对的曲线。